續前文,自從找到數列 A273889 後,端午假期有空就再尋找數式之間的關連,以大寫 B(n,k) 表示多重階乘的相加後的商數,
從這公式找到了數列 A274119,網友 z423x5c6 發現 IBM 的研究員 Chai Wah Wu 受到 A273889 證明的啟發又找出數列 A273983,表示這系列數列的新發現受到專家肯定,而我也從這裡找到類似 B(n,k) 的性質,另外定義小寫 b(n,k) 表示多重階乘的相減後的商數,
導出公式後,很快就登記數列 A274136 (申請中),不過總覺得分兩個數式 B(n,k) 及 b(n,k) 很麻煩,想能不能再整合成一個?仔細看這兩式結構相近,因此想出下式更為簡潔優美,
想出上式後,又再想有沒有通式可以整除,結果還真被我想出來,
B(n,0,2,1) = A001045(n+1) = 1, 1, 3, 5, 11, 21, 43, 85, ...
B(2*n,0,2,1) = A007583(n) = 1, 3, 11, 43, ...
B(2*n+1,0,2,1) = A002450(n+1) = 1, 5, 21, 85, ...B(n,1,2,1) = A152663(n) = 1, 1, 6, 16, 120, 540, 5040, 32256, ...
B(2*n,1,2,1) = A009445(n) = 1, 6, 120, 5040, ...
B(2*n+1,1,2,1) = A274136(n) = 1, 16, 540, 32256, ...
B(2*n,2,2,1) = A273889(n+1) = 1, 9, 435, 52017, ...
B(2*n+1,2,2,1) = A273983(n+1) = 1, 31, 2745, 487935, ...
B(2*n,3,2,1) = A274117(n+1) = 1, 12, 1064, 252160, ...
B(0,n,2,1) = A000012(n) = 1, 1, 1, 1, ...
B(1,n,2,1) = A000012(n) = 1, 1, 1, 1, ...
B(2,n,2,1) = A008585(n+1) = 3, 6, 9, 12, ...
B(3,n,2,1) = A100040(n+2) = 5, 16, 31, 50, ...
B(4,n,2,1) = A274119(n) = 11, 120, 435, 1064, ...
目前已知特性如下,
B(n,-k,-a,-b) = (-1)^(n+1) * B(n,k,a,b)
B(n,k,b,a) = (-1)^(n) * B(n,k,a,b)
B(0,k,a,b) = 1
B(1,k,a,b) = a - b
下面是這通式整除的證明,
找出這些數學式的感想為,以前大家都是尋找一維的數列變化,但以後可能會出現很多這類二維數列 (數列之間的關係),這算是 Bridan Formula 的創舉,暑假有興趣的朋友可以嘗試用 B(n,k,a,b) 尋找質數數列,因為到目前為止,還沒有人可以完整找到質數數列,如果你找得到,數學史絕對會記錄你的大名,以前大家都是用多項式尋找,現在多了一樣工具,或許可以挖到寶藏,從別人的研究再發現,科技的發展就是這樣慢慢進步的。
延伸閱讀:慶賀 OEIS A273889 數列申請成功、Bridan Formula ─ 最新發現數論特性、OEIS A274119 數列的故事

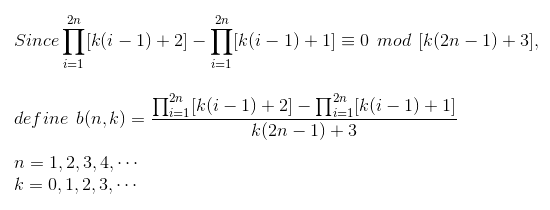

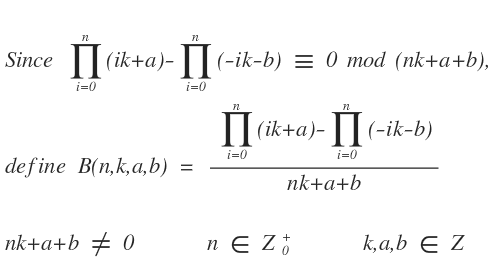
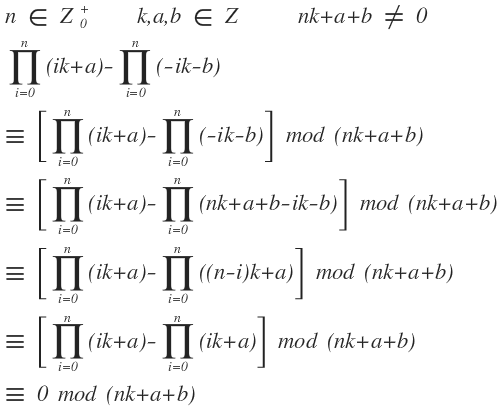







沒有留言:
張貼留言