魔術方塊是 20 世紀偉大的發明之一,幾乎每個人青少年時期,都玩過或見過這個玩具,其解法有許多人研究,通常多數人是把解法公式背起來,不知其原理,近日在網路上看到三階魔方展開圖 (上圖左),就很容易明白解法。
2022年12月31日 星期六
2022年12月27日 星期二
2022年12月23日 星期五
2022年12月19日 星期一
訓練數學感 338 ─ 可樂瓶改裝
niji.journey 咒文 - 改造可樂罐頭
網友行天下發現可口可樂將鋁罐改裝後,瓶身變瘦高並且價格調漲,因此他測量鋁罐外圍尺寸,從 65 mm (直徑) x 115 mm (高) 改成 57 mm (直徑) x 147 mm (高),飲料都裝 330 ml 沒有改變,請問你對這樣改變的看法?如果你是產品設計師,你認為甚麼尺寸最符經濟效益?
難度 ✩✩
2022年12月15日 星期四
ChatGPT
2022 年 12 月最火的網路事件應該是 ChatGPT,一個能夠聊天的 AI,你給它一個對應的語言,它能以該語言回應你,姑且不評論回應內容是否正確,但是它給出的答案還蠻有條有理,雖然不盡完美但是有人類回應的感覺,不會有機器回應死板板的感覺。
2022年12月11日 星期日
2022年12月7日 星期三
Git (Bitbucket + Sourcetree)
2022年12月3日 星期六
重回研發
在 2020 年,當時研發單位沒有新案子可以效力,因此我從研發部門調動到商業發展部擔任技術支援,負責的產品是多年前偕同開發的儀器,雖然早已熟悉,但是它的系統控制軟體極為複雜,主要應用於 CIS (CMOS Image Sensor) 晶片檢測上,調任我是因為個人有軟體背景,學習以及理解系統程式,不必花太多力氣訓練我,雖然遭遇 COVID-19 流行,負責帶我的工程師遠在日本,不過透過網路仍然可以遠端指導,再加上是支援台灣本地協力廠商,因此很快適應這份工作,從第一年許多事陌生,第二年可以直接回覆協力廠商 AE 們一半以上的技術問題,到現在已經駕輕就熟,全權負責台灣區域該產品技術諮詢,合作多年的日本工程師明年也將調任其他部門,在此非常感謝他的努力付出,留下技術寶典給我,可以應付各方技術難題。
2022年11月29日 星期二
2022年11月25日 星期五
從黃武雄自傳看如何學數學
前些日子在網路上看到一篇台大數學教授黃武雄先生自傳,刊登於數學傳播 42 卷 1 期,文章中有兩個段落關於數學學習值得提出分享。
一個是第 5 頁的 (3.5)「起惑點」,數學的學習像是石頭一塊又一塊疊上去,你某個單元沒有搞通,基礎就會不穩固,要怎樣才能繼續向上進步?就是回到你不懂的地方「起惑點」從新開始,因此除了極少數的人,最後幾乎都可以弄懂,每個人資質不同,天才的人很快學會,大鳥慢啼的要久一點時間學會,只是學校因進度安排無法等待所有人跟上,所以容易造成落後者落後太多而放棄。如果你有時間又想重獲數學能力,就是回到「起惑點」重新出發。
另一個是第 13~15 頁的 (7.3) 教材擺盪,一份好的教材應該淺中深三種程度內容並列,並標註內容難度,不同程度的人可以根據自身狀況學習,這樣不會讓程度佳的同學覺得枯燥沒挑戰性,程度差的不會說怎麼沒有一個看得懂,現在我們的學校教材基本上放中等程度的內容,然後刪除較艱澀的部分,對程度差的同學沒有補救內容,每次教材改編總是在難易之間擺盪,只治標不治本。這我深有同感,小時候家中有很多書籍雜誌,很多我都看不懂,但是我可以任意取之閱讀,久而久之慢慢理解內容,最後都成為我未來知識的種子,所以教科書內容難易並呈給讀者自己選擇是比較好的。
2022年11月21日 星期一
2022年11月17日 星期四
訓練數學感 335 ─ 綠色面積
2022年11月13日 星期日
dB 相關單位
前些日子在 MakerPRO 看到「一次搞懂dB的衍伸單位」這篇科技專文,讓我想起以前曾寫過 dBm 之類計算程式,通常弄過音響或測量聲壓的人才會遇到 dB 相關計量。目前使用的單位有以下幾種:
最原始的定義,需要一個參考量 $value_{ref}$
$dB = 10\times log_{10}(\frac{value}{value_{ref}})$
SPL (Sound Pressure Levels),聲壓參考值 $2\times 10^{-5}\;Pa$
$dB = 10\times log_{10}(\frac{P^2}{P^2_{ref}})=20\times log_{10}(\frac{P}{P_{ref}})$
$dBSPL = 20\times log_{10}(\frac{P}{2\times 10^{-5}})$
測量聲音功率以 1mW 為基準
$dBm = 10\times log_{10}(\frac{P}{1\times 10^{-3}})$
測量電壓以輸入阻抗 600Ω 及 1mW 為基準
$P=\frac{V^{2}}{R}$
$dBu = 20\times log_{10}(\frac{V}{0.775})$
測量電壓以輸入阻抗 1000Ω 及 1mW 為基準,也就是 1V 為新基準
$dBV = 20\times log_{10}(\frac{V}{1})$
dBFS (Decibels Full Scale),0 dBFS 以設備最大音量為基準,假設數位 16 bits
$dBFS = 20\times log_{10}(\frac{sample}{65536})$
RF 領域的功率單位,以 1 mV(rms)為基準,不過實際功率會依照系統阻抗而不同
$dBmV = 20\times log_{10}(\frac{Volt}{1mV})$
RF 領域的功率單位,以 1 uV(rms)為基準,不過實際功率會依照系統阻抗而不同
$dBuV = 20\times log_{10}(\frac{Volt}{1\mu V})$
dBc 以載波(Carrier)的功率為基準,衡量諧波或 phase noise 相對於載波的功率
2022年11月9日 星期三
2022年11月5日 星期六
訓練數學感 334 ─ 邏輯推理
2019 年大陸刑偵科推理試題,十個單選題為一題組,
(A) A (B) B (C) C (D) D
(A) C (B) D (C) A (D) B
(A) 第三題 (B) 第六題 (C) 第二題 (D) 第四題
(A) 第一、五題 (B) 第二、七題 (C) 第一、九題 (D) 第六、十題
(A) 第八題 (B) 第四題 (C) 第九題 (D) 第七題
(A) C (B) B (C) A (D) D
難度 ✩✩✩
2022年11月1日 星期二
2022年10月28日 星期五
競爭與變化的年代
「產銷人發財」在企業管理方面是五個重點管理項目:
生產與作業管理 (Production and operation management) ─
生產是將各種投入資源轉換成最終產品或服務的過程。
行銷發掘消費者實質或潛在需求,並透過各種方法加以滿足的過程。
配合組織的各項策略及各項作業需要,適時地提供適質適量的人力。
配合組織策略需求,維持組織的產品及製程在一定水準之上,以求提昇企業之競爭力。
配合組織各項作業需要,找尋適當的資金來源,以最低的資金成本滿足組織資金需求,並將風險控制在可以接受的範圍內。
2022年10月24日 星期一
再談 APCS
每年底學測前,總是興起準備 APCS 考試的話題,因為近日看到金門大學陳鍾誠教授挑起這議題,想說說自己的看法。先說,我是已經 36 年程式設計資歷的工程師,相當清楚如何入門學習程式設計、遭遇困難問題如何逢凶化吉,以及程式工作的職涯發展,另外,自己的小兒也正在讀交大資工,在此分享我們的經驗。
我的心得是,一輩子走程式設計這條路,不是人人都有辦法一直走下去,因此應該要先審視自己的個性,程式人通常有以下特點:
一、愛好自學 ─ 電腦科技日新月異,三不五時會有新技術、新語言、新工具出現,因應需求有時被迫更換使用新東西,非愛好學習者,通常承受不住這種壓力,我寫了三十多年程式,到現在還是經常在學東西,不只程式語言,更多的是跟程式無關的,因為有時解決問題的靈感來自其它領域的知識。學習方法不外乎老師教授以及自己學習,老師教的最大好處,快速有系統地把知識傳授給你,但是你的腦子能否快速吸收這些大量知識,那又是另一回事,很多知識是需要基礎的,如果少了這些先備知識,是無法充分理解應用的,況且有些問題是不明的,因此自己要訓練自己有自學能力,能夠成為自己的老師,分析問題原因,可用的對策有哪些,否則卡關無法突破,你就會想要轉職,個人認為時間花在補習上,你就少了時間訓練自學。
二、理性思考 ─ 越理性的人,邏輯思路通常越清晰,邏輯越清晰,寫出來的程式出錯的機會就越少,品質也越好。程式除錯時也非常需要縝密的抽象思考,甚至要有觀察力、想像力,當程式出現異常時,我會先觀察問題現象,根據線索釐清問題,想像以及假設程式處在某種狀況才導致問題,從這些地方下手多數可以迎刃而解,當然也曾遇過要同時改善三五個地方才能解決的,甚至也碰過不可能的任務 ─ 控制不可控制的系統,這些都需要像偵探般細心判案才能解決問題,個人覺得棋奕類的遊戲是訓練抽象思考很好的工具。不善於理性思考的人,寫出來的程式出錯率極高,光除錯就把自己搞死了,你就不會想當程式設計師了。
三、耐性沉著 ─ 人非先知聖人,程式總有寫錯的時候,此時需要除錯,這也是最考驗耐性的時刻,如果你能一邊寫一邊測試,那是最好的,因為可以容易立即發現錯誤並修正它,不過這也會造成進度緩慢,因為有些程式一直被重複測試浪費時間。那一次全部寫好再測試不就好了?如果這麼做,複雜系統可能無法立即發現錯誤點在哪裡,需要程式碼一個區塊一個區塊檢查,有時還看不出問題點,學生時代,我曾用一個禮拜時間寫出約 1000 行組合語言程式碼,結果用三個禮拜的時間除錯,經過那次教訓後,就採用邊寫邊測的方式設計程式,雖然程式設計進度不快,但是成功率提高很多。因此耐性沉著是程式人非常關鍵特質,少了它,你撐不久。
2022年10月20日 星期四
2022年10月16日 星期日
How great leaders inspire action | Simon Sinek
2022年10月12日 星期三
完整非電腦證明考拉茲猜想 (五) (Collatz conjecture 5)
續前文(四),雖然在 2019 年並未成功證明考拉茲猜想,不過近期有新的思路嘗試想再次證明它,這一次把數值十進位轉換成二進位,就比較容易解析與理解。
2022年10月8日 星期六
訓練數學感 332 ─ 倒藥水
有一個大桶子裝滿藥水,它的容量不清楚,倒出 10 公升藥水後,再裝滿純水稀釋,充分混合後再倒出 8 公升再加入純水裝滿,此時桶子內藥水與純水比例 3:2,請問這桶子有多大?
難度 ✩✩
2022年10月4日 星期二
數學雜談
行天下是在我部落格上認識的網友,他的專業在數學,而我是數學愛好者,因此偶而會聊聊數學,近日聊到數學實數完備性,數學很在意證明及定義的嚴謹性,不能憑感覺證明,否則一但被人發現破綻,所有奠基在此之上的學問將一夕全毀,另外它也難在用數學的語言,描述及證明,古人從整數 (1, 2, 3, ...)、有理數 (1/2, 1/3, 1/4, ...)、無理數 (√2, ln 2, 𝞹, ...) 到微分連續性,把所有實數數線上漏洞逐一補齊。
2022年9月30日 星期五
資深程式設計師的工作經驗法則
前些日子在網路上看到一篇好文,在此紀錄分享,原文標題「有40年經驗的程式設計師把工作經驗整理成13條建議,希望能為新手提供幫助」,題目太長了,把它縮改成「資深程式設計師的工作經驗法則」。直接切入主題,看這 13 條建議是甚麼以及補述個人觀點:
當然越年輕開始越好,可以累積更多經驗,但是考量基礎知識的建立,建議高中左右年紀開始最好,再搭配高中數學一起學,能讓你如虎添翼。
寫程式就是為了解決問題,寫不同類型程式可以擴大解決不同類型問題經驗。
有時候學一些不太相關的東西,未來可能會用到。
對程式設計有熱誠才有辦法長久工作下,我非常同意原作者 Noah Gibbs 的吸引點,我喜歡寫程式給我帶來的成就感和聰明的感覺。
每個專案都可以讓你學到東西,但是它通常不會是一天兩天就搞定的,把它當日記記載你的想法,可以實踐你想法的日記。
對我來說,職業不是短期性的工作,它是有生涯目標的,我獲得這項能力,可以創造方便解決我生活或工作需求的東西。
重要的東西在你人生的道路上一定會出現,你需要它時就在當時盡力學習。
每一個人的經歷絕對不同,同樣十年二十年的時間價值是不同的,薪水也會不一樣,要自問這段時間你完成了甚麼專案,你能否帶領別人完成專案?這兩件事決定了你的價值。
寫程式的過程中,一定會有 實作、犯錯、學習、修正錯誤 的輪迴過程,不一定要從理論開始學起,只要你喜歡以及有效的方法,都可以讓你學到東西,不過最重要要實作出程式。
你需要學習各式各樣技術,也同時要學非技術技能,程式設計這一行,在除錯過程很需要洞察力。
當你沒有好方法設計程式解決問題時,可以參考其它領域專業方法如何處理問題。
這方面我和作者看法相異,初學者或是原理探究者,應該要重複造輪子,雖然多花了些時間,但是比較容易問題除錯。
燃燒你的熱誠,只要持續在程式設計這條路上,你就是程式設計師。
2022年9月26日 星期一
訓練數學感 331 ─ 四皇后
2022年9月22日 星期四
知心英文 聽力訓練
最近訓練聽力,看到知心英文影片,覺得應該要推薦給不知如何訓練英聽的學子參考,它每一個句子會播放四次,前兩次會遮蔽英文句子,後兩次則會顯示出句子,這樣子很適合初階學員練習,練聽力需要聽出句意。
2022年9月18日 星期日
2022年9月14日 星期三
這是我的,別想碰!(Mine!)
這是我的,別想碰!:「所有權」潛規則如何控制我們的生活?
Mine! : How the Hidden Rules of Ownership Control Our Lives.
王端徽,平安文化出版 ISBN 978-986-5596-97-2
2022年9月10日 星期六
2022年9月6日 星期二
正則表達式 (Regular Expression - Pythex)
暑假即將結束,Andy 終於開始碰電腦寫程式了,前兩個月每天瘋狂玩西洋棋,甚至自己找西洋棋教室當助教工讀,以及找國手指導棋藝,假日和一些棋友棋聚,不過現在想從 chess.com 和 LiChess 網站,利用爬蟲程式爬出棋局資料,我想這應該是不錯的專案練習。
對爬蟲程式完全沒概念的他,我跟他說明網頁原始碼概念後,一天內就學會用 Python 抓出網頁原始碼,而解析網頁內容,他選擇正則表達式來處理,這已經超乎我的經驗與專長,本文主要做一個紀錄,有這麼一個東西,它可以更有效率處理字串,以後設計網路爬蟲程式不必再字串搜尋與擷取用土炮方法處理,回想二十年前個人就是這樣弄雅虎奇摩基金爬蟲程式。
2022年9月2日 星期五
參數測試 (Parametric Testing)
近日工作遇到專業名詞定義問題,參數測試即其中一例,在半導體測試方面常用於 DC parametric testing,例如 Vth, Ids, Idoff 和 Cox 等,即使電容量測使用 AC 技術。
相對應的 Non-Parametric Testing 指的是 Go/No-Go 的判別類型測試。
2022年8月29日 星期一
訓練數學感 330 ─ 擺放最大正方形
2022年8月25日 星期四
2022年8月21日 星期日
2022年8月17日 星期三
訓練數學感 329 ─ 山羊吃草
有一隻羊在羊圈內,羊圈的半徑為 R,這隻羊綁了一條長度為 r 的繩子固定在羊圈柵欄某固定位置。
請問這繩子多長,剛好可以讓山羊吃草面積與沒吃到的地方,面積相等?
希望繩長 r 以 羊圈半徑 R 來表示。
難度 ✩✩✩✩
2022年8月13日 星期六
數學之美 13 ─ 餘弦定理 (Law of cosines)
2022年8月9日 星期二
奈米電子學 (Nanoelectronics)
Nanoelectronics - Devices, Circuits and Systems
Part I Device Modeling and Applications
Ch 1: Tunnel FET: Devices and Circuits
Ch 2: Electrothermal Characterization, TCAD simulations,
and Physical Modeling of Advanced SiGe HBTs
Ch 3: InP Based High-Electron-Mobility Transistors for High-Frequency Applications
Ch 4: Organic Transistor- Device Structure, Model and Applications
Part II Spintronics
Ch 5: Mitigating Read Disturbance Errors in STT-RAM Caches by Using Data Compression
Ch 6: Multi-Functionality of Spintronic Materials
Part III Optics and Photonics
Ch 7: Photonics Integrated Circuits
Ch 8: Graphene Based Optical Interconnects
Part IV Plasmonics
Ch 9: Hot Carrier Generation in Plasmonic Nanostructures: Physics and Device Applications
Ch 10: Plasmonic Metamaterial-Based RF-THz Integrated Circuits: Design and Analysis
Part V Emerging Materials
Ch 11: Advances in InSb and InAs Nanowire Based Nanoelectronic Field Effect Transistors
Ch 12: Carbon Nanotube and Nanowires for Future Semiconductor Devices Applications
Ch 13: Role of Nanocomposites in Future Nanoelectronic information Storage Devices
2022年8月5日 星期五
訓練數學感 328 ─ 統計檢定
近日一則新聞,提及手機遊戲玩家丁特,想製作稀有寶物「紫布」,進行471次製作卻只有11件成功,與廠商宣稱 10% 成功機率有很大差別,請以統計檢定方法證明廠商宣稱的資料是正確還是錯誤的。
難度 ✩✩✩✩
2022年8月1日 星期一
2022年7月28日 星期四
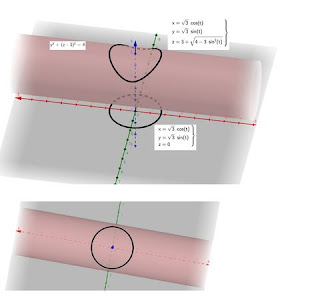
訓練數學感 327 ─ 圓柱上的圓形
2022年7月24日 星期日
明知山有虎偏向虎山行,需要勇氣與智慧
近日突發奇想,想製作簡單的 5V 邏輯電路,不想使用 IC,應用於教育場合,因此在 Arduino.Taipie FB 社團詢問網友們推薦熟悉的 NPN, PNP TO-92 電晶體型號,而得到諸多意見參考。
其實個人是熟悉電子電路設計的,不過專長偏重在韌體設計,太久沒使用晶體元件了,故請網友們提供熟知元件編號,經過規格書比對,個人偏好桃園賴桑推薦的 2N3904, 2N3906。
此外,不少網友點出使用電晶體去兜邏輯電路是自找麻煩,沒錯這 side project 就是在找麻煩,明知山有虎偏向虎山行,這需要勇氣與智慧,它是我有興趣做的硬體專題,會花點時間去搞,弄這個會有點像用樂高積木去製作一個作品,作品完成前,甚麼都不是,但是完成後,會讓很多人拍拍手。
2022年7月20日 星期三
西洋棋殘局 3 ─ (Endgame 3 of Chess) 及 lichess 介紹
2022年7月16日 星期六
訓練數學感 326 ─ 求半徑
2022年7月12日 星期二
數學之美 12 ─ 根號數
https://www.facebook.com/photo?fbid=2901082166862737&set=a.1462097617427873
圖片來自 FB 社團,這兩圖常見於根號數尺規作圖,右圖還方便計算 $\sqrt{5} - \sqrt{3}$ 之類算式。
2022年7月8日 星期五
2022年7月4日 星期一
訓練數學感 325 ─ 階乘平方數
1! x 2! x ... x 19! x 20!
從 1! 到 20! 連續相乘,但是只要拿到其中某一個階乘會讓其數值變成平方數,請問是哪一個?
難度 ✩✩✩
2022年6月30日 星期四
投資心法
這陣子不知為什麼,FB 又出現一堆想加我朋友的人,其中不乏股友社助理,我挑明地告訴她們,給我 LINE ID,我將檢舉以及封鎖她們,多數人就此打住不再騷擾,在此分享個人投資心法,它不一定適合每個人,但是它適合我,原則不複雜:
我是不看股票的,但求穩定收息,因此
不限標的,定期買,績效不好就換,需錢時再賣。
隨時間推移,收入會越來越多,這些資金通常就是分散存放在可以安心並產生被動收入的地方,
沒事就不要經常搬動,除非能確定搬到某個地方會更好,否則我的時間心力是放在提升個人能力或創作感興趣的事物上。
靠消息來理財,有時雖然會帶來意外之財,但容易頻繁交易,而賺的錢會賠在手續費上或消息慢一步,自己瞎忙只是幫人抬轎。
這陣子比特幣等網幣急升又大貶,導致許多投資人損失慘重,網幣只有信徒在支撐,它沒頂也沒底,因此升貶幅度極為巨大,不宜全部身家投入,而各國貨幣雖然與金本位脫鉤,但是有政府財政支撐而有保障,除非政府破產,該貨幣才會不值錢。
2022年6月26日 星期日
2022年6月22日 星期三
組織改造
世界沒有永久不變的公司組織,它會隨不同人數,不同想法,不同任務編組而變來變去,沒有一定好壞,只是適不適合。
2022年6月18日 星期六
訓練數學感 323 ─ Coffee Scam
同學 LINE 群組傳了一段影片,有大中小三個紙杯,可是把咖啡倒到任一個紙杯,都剛好滿到杯口,有人說那是把小杯套在中杯和大杯裡面,除此之外,另一種方式,大的杯子比較瘦,讓這些杯子的總體積是相等的,現在某廠商使用第二種方式設計杯子,如果,小杯杯口直徑 9 公分,杯底直徑 6 公分,杯高 10 公分,假若中杯杯口直徑一樣,杯高 12 公分,請問杯底直徑多少?
難度 ✩✩✩
2022年6月16日 星期四
BBS 1-1.03 開叫分類與通則
1C | 12-17 點,不保證梅花張數 (迫叫一圈),可能包含下列情況之一 12-14 點,平均牌再蓋叫無王 或 非平均牌型再蓋叫花色 15-17 點,再跳叫四張以上牌組 或 無王 (門門有擋) |
1D/H/S | 12-14 點,牌組最少五張以上 |
1NT | 15-17 點,沒有五張高花的平均牌型,可能一門沒擋 若有五張高花但沒有大牌也可以 |
2C | 18 點以上,不保證梅花張數 (迫叫一圈),可能包含下列情況之一 18-20 點,平均牌再蓋叫無王 或 非平均牌型再蓋叫花色 21 點以上,再跳叫四張以上牌組 或 無王 (門門有擋) 或 超級強牌 |
2D/H/S | 18-20 點,牌組最少五張以上 |
2NT | 21-23 點,沒有五張高花的平均牌型,可能一門沒擋 若有五張高花但沒有大牌也可以 |
3C-3S | 正常阻塞叫,依照二三定律,至少六張以上牌組 |
3NT | 24-26點,平均牌型,門門有擋,無五張牌組 若有五張牌組則通常有滿貫,應先強二開叫 |
4C-4S,5C/D | 四線至少七張,五線至少八張牌組,阻塞叫 |
開叫邏輯:
12 點以上開叫,先確認是否為平均牌,若符合, 先開叫 1NT/2NT/3NT。
21 點以上一律開叫 2C。
花色開叫需五張以上,兩門花色時先開叫較高級花色,一階點力限定 12-14 點,二階點力限定 18-20 點。
梅花開叫會含括未被歸類的點力牌型,因此迫叫一圈,牌情需等待開叫者再叫。
三階以上阻塞性開叫,遵照二三定律,即被敵方賭倍,有身價最多倒二,無身價最多倒三 (敵方有局情形時),亦即三階開叫有6-7贏墩,四階開叫則需有7-8贏墩
第一二家阻塞性開叫,應基於堅強王牌 (至少5贏墩) 以及旁門花上不超過一個防禦贏張,並且不會有旁門的四張高花
第三四家開叫低花不得為輕開叫,輕開叫只限於高花,開叫者10點以上,高花五張以上
第四家開叫,應符合十五定律,即大牌點加黑桃張數大於等於15以上,才可以開叫
各種牌型與點力範圍之建議開叫叫品:
點力範圍 | 12 - 14 | 15 - 17 | 18 - 20 | 21 - | 24 - 26 |
建議開叫 | 1C/D/H/S 再蓋叫 花色或無王 | 1C/D/H/S/NT 再跳叫 花色或無王 | 2C/D/H/S 再蓋叫 花色或無王 | 2C/D/H/S/NT 再跳叫 花色或無王 | 3NT (門門有擋) |











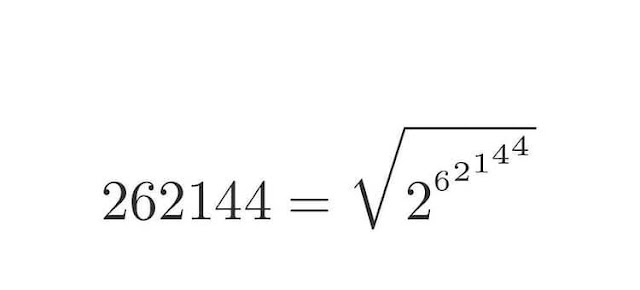



.webp)