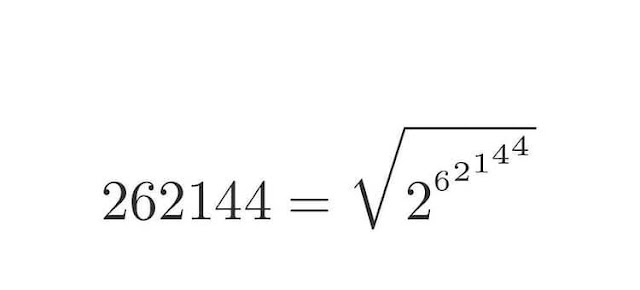訓練數學感 336 ─ 四隻鴨子

https://4rdp.blogspot.com/2022/11/336.html

題目如左，請求出四隻鴨子出現在同一半圓內的機率？

難度 ✩✩✩

閱讀更多 >>

從黃武雄自傳看如何學數學

https://4rdp.blogspot.com/2022/11/blog-post.html

前些日子在網路上看到一篇台大數學教授黃武雄先生自傳，刊登於數學傳播 42 卷 1 期，文章中有兩個段落關於數學學習值得提出分享。

一個是第 5 頁的 (3.5)「起惑點」，數學的學習像是石頭一塊又一塊疊上去，你某個單元沒有搞通，基礎就會不穩固，要怎樣才能繼續向上進步？就是回到你不懂的地方「起惑點」從新開始，因此除了極少數的人，最後幾乎都可以弄懂，每個人資質不同，天才的人很快學會，大鳥慢啼的要久一點時間學會，只是學校因進度安排無法等待所有人跟上，所以容易造成落後者落後太多而放棄。如果你有時間又想重獲數學能力，就是回到「起惑點」重新出發。

另一個是第 13~15 頁的 (7.3) 教材擺盪，一份好的教材應該淺中深三種程度內容並列，並標註內容難度，不同程度的人可以根據自身狀況學習，這樣不會讓程度佳的同學覺得枯燥沒挑戰性，程度差的不會說怎麼沒有一個看得懂，現在我們的學校教材基本上放中等程度的內容，然後刪除較艱澀的部分，對程度差的同學沒有補救內容，每次教材改編總是在難易之間擺盪，只治標不治本。這我深有同感，小時候家中有很多書籍雜誌，很多我都看不懂，但是我可以任意取之閱讀，久而久之慢慢理解內容，最後都成為我未來知識的種子，所以教科書內容難易並呈給讀者自己選擇是比較好的。

閱讀更多 >>

數學之美 17 ─ 不可思議的分數 (二)

https://4rdp.blogspot.com/2022/11/17.html

網路上看到，立即蒐錄。

閱讀更多 >>

訓練數學感 335 ─ 綠色面積

https://4rdp.blogspot.com/2022/11/335.html

邊長為 10 的正方形，內部有一個綠色區塊，由兩個半圓以及一個 1/4 圓弧線所包圍，試求綠色區塊面積。

難度 ✩✩✩

閱讀更多 >>

dB 相關單位

https://4rdp.blogspot.com/2022/11/db.html

前些日子在 MakerPRO 看到「一次搞懂dB的衍伸單位」這篇科技專文，讓我想起以前曾寫過 dBm 之類計算程式，通常弄過音響或測量聲壓的人才會遇到 dB 相關計量。目前使用的單位有以下幾種：

最原始的定義，需要一個參考量 $value_{ref}$
$dB = 10\times log_{10}(\frac{value}{value_{ref}})$

SPL (Sound Pressure Levels)，聲壓參考值 $2\times 10^{-5}\;Pa$
$dB = 10\times log_{10}(\frac{P^2}{P^2_{ref}})=20\times log_{10}(\frac{P}{P_{ref}})$
$dBSPL = 20\times log_{10}(\frac{P}{2\times 10^{-5}})$

測量聲音功率以 1mW 為基準
$dBm = 10\times log_{10}(\frac{P}{1\times 10^{-3}})$

測量電壓以輸入阻抗 600Ω 及 1mW 為基準
$P=\frac{V^{2}}{R}$
$dBu = 20\times log_{10}(\frac{V}{0.775})$

測量電壓以輸入阻抗 1000Ω 及 1mW 為基準，也就是 1V 為新基準
$dBV = 20\times log_{10}(\frac{V}{1})$

dBFS (Decibels Full Scale)，0 dBFS 以設備最大音量為基準，假設數位 16 bits
$dBFS = 20\times log_{10}(\frac{sample}{65536})$

RF 領域的功率單位，以 1 mV（rms）為基準，不過實際功率會依照系統阻抗而不同
$dBmV = 20\times log_{10}(\frac{Volt}{1mV})$

RF 領域的功率單位，以 1 uV（rms）為基準，不過實際功率會依照系統阻抗而不同
$dBuV = 20\times log_{10}(\frac{Volt}{1\mu V})$

dBc 以載波（Carrier）的功率為基準，衡量諧波或 phase noise 相對於載波的功率

閱讀更多 >>

PRDI 矩陣

https://4rdp.blogspot.com/2022/11/prdi.html

看到一篇 主管賞罰要公平，但帶人要「偏心」文章寫得很好，留文記錄。

作者所指的偏心，就是將下屬分四類因材施教，如左圖所示。

閱讀更多 >>

訓練數學感 334 ─ 邏輯推理

https://4rdp.blogspot.com/2022/11/334.html

2019 年大陸刑偵科推理試題，十個單選題為一題組，

一、這題答案是： 
(A) A   (B) B   (C) C   (D) D

二、第五題的答案是： 
(A) C   (B) D   (C) A   (D) B

三、以下選項中那一題的答案與其它三項不同： 
(A) 第三題   (B) 第六題   (C) 第二題   (D) 第四題

四、以下選項中那兩題的答案相同： 
(A) 第一、五題   (B) 第二、七題   (C) 第一、九題   (D) 第六、十題

五、以下選項中那一題的答案與本題相同：
(A) 第八題   (B) 第四題   (C) 第九題   (D) 第七題

六、以下選項中那兩題的答案與第八題答案相同：

(A) 第二、四題   (B) 第一、六題   (C) 第三、十題   (D) 第五、九題

七、在這十題中，被選中次數的最少的選項字母為：
(A) C   (B) B   (C) A   (D) D

八、以下選項中那一題的答案與第一題的答案在字母中不相鄰： 

(A) 第七題   (B) 第五題   (C) 第二題   (D) 第十題

九、已知“第一題與第六題的答案相同” 與 “第 X 題與第五題的答案相同” 的真假性相反，那麼 X 為：

(A) 第六題   (B) 第十題   (C) 第二題   (D) 第九題

十、在此十道題中，ABCD 四個答案出現次數最多與最少的差為：

(A) 3   (B) 2   (C) 4   (D) 1

難度 ✩✩✩

閱讀更多 >>

數學之美 16 ─ 整數與指數

https://4rdp.blogspot.com/2022/11/16.html

 

這張圖在 FB 看到，難以想像的巧合。

閱讀更多 >>