現在提出第二種輔助線，讓大家試看看能不能解出來？畫一線段 OB 經過圓心 E，與線段 CF 相垂直於 L，令線段 FL 長度為 k，線段 BL 長度為 n，可得方程式
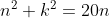
這個方法是我的小朋友想出來的，看大家能否利用這樣的線索來解題。
圓冪定理
-
圓冪定理包括相交弦定理，割線定理，切割線定理。 相交弦定理 切割線定理 資料來源：
https://zh.wikipedia.org/zh-tw/%E5%9C%86%E5%B9%82%E5%AE%9A%E7%90%86
1 天前
我其中一個想法是與月蝕日蝕的模型類似。日偏蝕月偏蝕通常氣象局會說最大蝕分是幾%。
回覆刪除以這個例子，小圓是在 x=y 這條直線上面移動。
當B這點與小圓相切時，斜線區域面積為0，然後繼續往右上移動。面積應該會與移動距離成某種函數。
這是我的其中一個想法。但還有後續的推導要繼續下去。
好有趣的比擬，這個日月蝕面積變化，應該與上述方程式有相關連。
刪除這題小圓的圓心 E，其實距離原點在 5sqrt(2) 的位置，BCF大弧小弧圍成的新月月形面積都是相等的。
刪除例如把小圓圓心移到 (5sqrt(2),0)，新月面積是等於BCF的。其他，我要再想想。
嗯，我懂你的意思，將 OE 線段以 O 為圓心旋轉，BCF 新月面積是相等的，讓 E 落於 X 軸，然後調變 E 點去求新月面積大小，找出它的通式。
刪除哇，又是一樁難題!
刪除非常值得探討，等段考完再來研究研究。
有大家踴躍參與，讓部落格增色許多，謝謝，通解當作進階題，
刪除祝你段考順利！
請問為什麼是20n?
回覆刪除第二式是從第一式展開推導而來。
刪除其實n,k都是可以算出來的!
回覆刪除比如說，線段OE=5sqrt(2)，所以線段EL=10-5sqrt(2)-n
(EL)^2+k^2=5^2
[5sqrt(2)-n]^2+k^2=25
這樣就有另外一個方程式了。
我當時的解法是，透過觀察三角形OCE，其實三個邊長都可以算得出來。這時CL=k作為高就可以被求出，與海龍公式證明初期使用畢氏定理算高的方法相同，即可求出k，後用十減之，又得n。
更正小錯誤，應該是
刪除[10-5sqrt(2)-n]^2+k^2=25
http://imgur.com/OdZa5t4
回覆刪除推導得不錯，過程我並未仔細查看，直接代公式 A(5,10)，兩個 arccos 數值都對，不過第三項看不到 25sqrt(7)/2，這部分需要再檢查。
刪除發現是前面的負號提出與[sqrt(2)+1]^2的計算出了問題。
刪除公式的第三個乘項(也就是四邊形COFE)應改為
(1/2)sqrt[(-1)(r^4-6r^2R^2+R^4)]
代入(r,R)=(5,10)，可得25sqrt(7)/2。
※其實中間的四次式是可以因式分解為二次式的，不過於實際運算上沒有太大助益(我是這麼覺得)：
sqrt[(-1)(r^2-2rR-R^2)(r^2+2rR-R^2)]
很高興你解題出來，謝謝，不過，熬夜就太拼了，睡眠很重要。
刪除那一天晚上點就睡了......半夜醒來沒事做，就著手來解這題了。
刪除七點
刪除原來如此，應該是準備段考太累了。
刪除這個題目的解題技巧，竟然可以用在困擾我多年的問題上：
回覆刪除交於兩點兩圓之重疊面積公式
設圓O1:(x-x1)^2+(y-y1)^2=r1^2
圓O2:(x-x2)^2+(y-y2)^2=r2^2
且r1+r2>sqrt[(x1-x2)^2+(y1-y2)^2]=O1O2=a
s=(1/2)(r1+r2+a)
兩圓重疊面積為
r1^2arccos[(1/2r1a)(r1^2-r2^2+a^2)]+r2^2arccos[(1/2r2a)(r2^2-r1^2+a^2)]-2sqrt[s(s-r1)(s-r2)(s-a)]
沒想到你還能進一步，把這題目轉化為求解兩圓交疊面積，這是一次成功的推導。
刪除進階題，已知小圓r半徑，n,k長度，求兩圓相交面積？
刪除畢氏定理：
刪除(R-n)^2+k^2=R^2
R^2-2nR+n^2+k^2=R^2
R=(n^2+k^2)/2n
再代入公式即可。
上述畢氏定理的列式是相當經典的國三題目。
大圓R推導，與原題第二式同，看來需要 R,r,n,k 計算 a，才能求兩圓相交面積。
刪除$\LaTeX$
刪除